1、取整函数:
ceil() floor() int() rint() trunc() round()
ceil()取整函数,将小数部分省略,取整数值大一的值。 eg:ceil(6.1)=7;
floor()取整函数,将小数部分省略,只取整数部分。 eg:floor(6.1)=6 or floor(6.9)=6;
int()取整函数,将小数部分省略,只取整数部分。 eg:int(6.5)=6;
trunc()取整函数,将小数部分省略,只取整数部分。 eg:trunc(6.5)=6;
rint()取整函数,遵循四舍五入的取值原则。 rint(6.5)=7 or rint(6.1)=6;
round()取整函数,遵循四舍五入的取值原则。 round(6.5)=7 or round(6.1)=6;
取整函数大致分为这三种类型: 1)、ceil()将小数部分省略,取整数值大一的值。
2)、floor()、int()、trunc()取整函数,将小数部分省略,只取整数部分。
3)、rint()、round()取整函数,遵循四舍五入的取值原则。
取整函数还有一种是sign()函数
sign()函数是但参数变量为0时,取值为0,当参数变量取值为负数时,则取值-1,当参数
变量取值为正数时,则取值为1。她的取值空间就是-1,0,1。这个函数只能取三个状态值。
2、wrap()周期函数:
wrap()函数:可以做一个周期效果,产生周期性的分布效果,与求余有一样的效果。
wrap()函数的基本使用:wrap(变量,周期最小取值,周期最大取值)
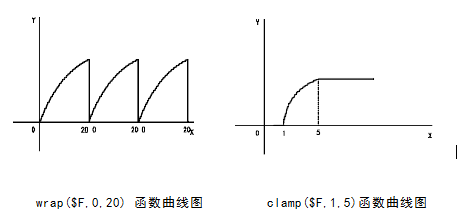
eg:wrap($F,0,20)
它的取值空间在1-20之间,当变量值大于20时,进入下一个周期,从1开始继续取值。
注意下wrap()函数和clamp()函数的函数曲线。唯一的区别在于wrap()函数拥有周期性的特点。
3、fit()函数,适配函数:
fit()函数拥有三种不同的适配方式
1)、fit01()函数
fit01(变量,新的范围最小值,新的范围最大值)
案例说明下
创建line节点,为line添加属性,这里创建一个attribcreate节点,添加一个以aaa命名的点属性,class:point(点属 性),value这里使用$BBX作为属性aaa的值,这也说明了属性aaa只能在0-1之间任意取值,当这里加入fit01()函数 时,fit01($BBX)这里的取值从0-1扩大到0-10的取值,fit01()函数对原有的取值范围进行均匀的映射。
只有在变量参数的取值范围在0-1之间是才可以使用fit01()函数进行映射取值。
fit01()函数针对的事原有变量是0-1的范围才可以是fit01()这个函数进行映射,按变量值在范围值内均匀取值。
2)、fit10(),fit01(),fit11()的映射取值的方式
fit10()函数的取值与fit01()函数的取值范围正好相反。
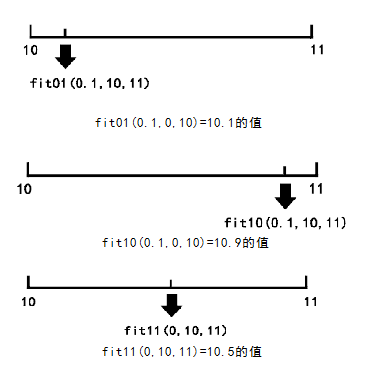
fit11()函数是从-1-1的取值范围进行取值。
这些fit()函数相对比较麻烦。现在用fit()函数代替以上几种fit()函数的形式
fit()函数的格式:fit(变量,原有的范围最小值,原有的范围最大值,新的范围最小值,新的范围最大值)
eg:
fit($PT,$NPT-1,0,1) 这样可以将取值规范化处理。
fit($PT,$NPT-1,0,10) 这样将取值的范围扩大了10倍。
4、distance() Houdini所特有的内置函数,用于测量两个点之间的距离。
先说明下distance()函数的使用:
先创建两个点用于测量,我们用Add节点,创建随机的两个点,计算了下两个点之间的距离值,将测量的距离值用font节点打印出来。
distance()函数的格式:
distance(X1,Y1,Z1,X2,Y2,Z2)也就是写入所需要测量的两个点的XYZ空间坐标。
我们这里通过前面的案例说明下distance()函数的使用:在font节点的text属性中写入distance(),将测量的距离结果打印出来。
表达式:
`distance(point("../add1",0,"P",0),point("../add1",0,"P",1),point("../add1",0,"P",2),point("../add1",1,"P",0),point("../add1",1,"P",1),point("../add1",1,"P",2))`
5、length()函数用于求线段的长度值或者向量的值。
这里用一个案例说明下lenght()函数来求速度的大小。
创建一条线段,给予线段一定点数量,方便做spring弹簧的解算效果。为通过spring解算过的线段添加属性,创建一个attribcreate节点,添加一个命名为speed的新属性,
value:length($VX,$VY,$VZ)使用lenght()函数计算。
创建sphere小球,通过copy节点,将小球拷贝到解算的线段上。在copy节点的Uniform scale的属性上调用前面新添加的属性:$SPEED/30 让小球根据lenght()函数计算出来的结果,对小球进行整体的缩放。
6、Normalize()函数的使用(标准化函数)
①、normalize()是一个标准化函数,使向量的长度值为“1”,只为了对向量的长度做一个标准化的控制。它不对方向进行控制,只是对长度保持一致,做规范化的处理,(向量由长度和方向构成的,Normalize()函数只是对长度值做修改)。
现在用案例说明下:
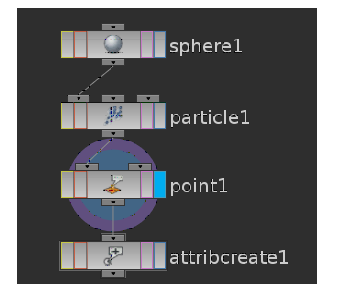
这里利用polygon sphere发射粒子,通过为粒子添加法线,将速度方向显示出来add normal :($VX,$VY,$VZ),添加一个新属性对速度的做一个标准化的处理。创建一个attribcreate节点,
name:(新属性的名称)normalvel ;type:(新属性的数据类型)vector创建一个向量类型;
value:(变量的数值)vector3($VX,$VY,$VZ);这里将分量写在vector3()的函数内,将三个分量合为一个向量,整体的表述出来。
②、法线,速度都是三元向量,使用 vector3()函数一次性的将向量表述出来,现在在对速度进行标准化处理。他表述的向量:normalize(vector3($VX,$VY,$VZ))
而在value中写入的是三个分量,那么如何将一个向量写入分量中。这里在向量的后面加入[0]将分量提取出来,这样就可以将向量以分量形式写入value中了。
value:
normalize(vector3($VX,$VY,$VZ))[0]
normalize(vector3($VX,$VY,$VZ))[1]
normalize(vector3($VX,$VY,$VZ))[2]
③、现在验证下速度的规范化处理,我们要的是要创建自定义向量属性normalvel的分量形式,才可以写入normal的三个框中。
在attribcreate的节点下再次创建point节点,添加法线属性,add normal:($NORMALVELX,$NORMALVELY,$NORMALVELZ),在变量之后加入X,Y,Z进行向量转分量的输入。
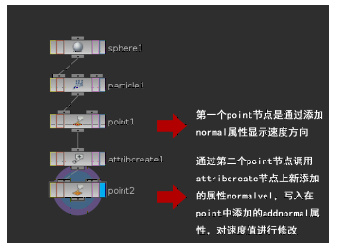
④、在houdini中,对于粒子速度的调整,要在particle节点之前使用,现在在particle节点之后使用$NORMALVEL向量修改速 度,显然是无法实现的,因为这是通过point节点对速度的修改,而不是通过节点解算得到的速度结果。在sop模块下,对速度的修改要在解算之前,不对解 算后的速度节点进行修改更新。
7、mindist()或者 pointdist()两个函数等价。都是求点到面的距离。
1、XYZdist()是空间点到面上的距离,这是与上面的两种函数的区别;
pointdist()函数的基本格式:
pointdist(“点所在节点的路径”,点序号,“面所在节点的路径”,面序号,通道号)
pointdist()函数输入的是点序号,算的是实际点到面上的距离值。这里的通道号,表示所求的属性,“0”代表的是求的点到面上的距离值,“1”代表的是所求面上落点的u方向的坐标值,“2”代表的是所求面上落点的v方向的坐标值。



