我们在houdini中制作如下效果会用到Copy节点:

节点连接如下图:
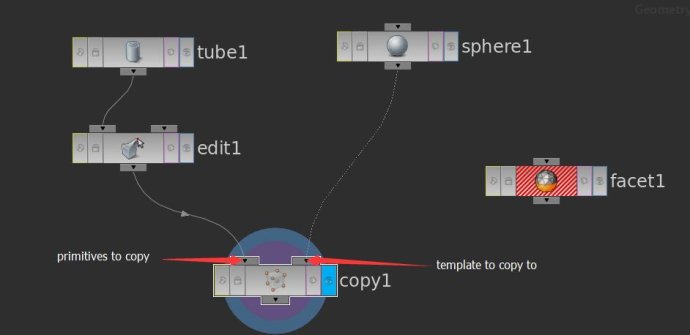
其中Copy节点分为左右两个输入口:左边的是primitives to Copy(需要复制的原型)。右边的是template to copy to(作为要被复制到的样板)。我们把锥形复制到圆球上,再把锥形的尖尖朝向Z轴

,那么就得到了一个刺球了(相对来说比maya要容易实现一点)。
过程中涉及到一个节点facet我并没有使用,这个节点的主要作用是处理法线相关的操作,并且Unique功能可以拆分面,让每个面都是独立的。我们借助下这个节点来分析下点法线与面法线。
1、什么是面法线
法线(normal line) 始终垂直于某平面的虚线。在数学几何中法线指平面上垂直于曲线在某点的切线的一条线。在三维软件中,我们一般认为面法线是垂直于平面的虚线。弧面的法线是垂直于弧面切线的虚线。
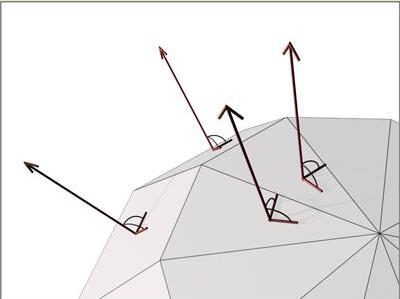
2、顶点法线
我们说一般一个顶点是没有法线的,一个单一平面上的点,它的法线方向与面法线一致。但是由多个平面拼接后相交顶点的法线应该如何确定呢?
下面蓝色线是houdini中box的八个顶点的法线方向:
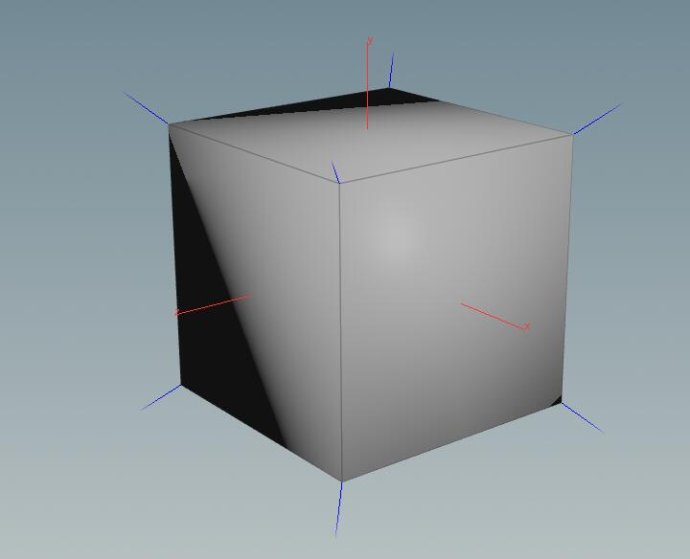
仿佛不难理解,但是追其根源,这个角度是怎么得来的呢?
首先我们利用Facet节点独立box的每一个面,我们发现box的每个顶点分出了三颗法线,方向呢我标记出来了,与它们所在的面法线方向一致:
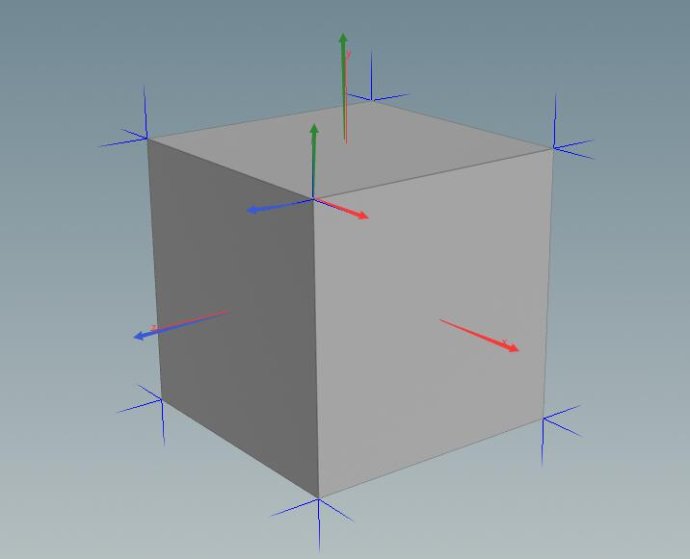
那么其实当三个面合并后,那个顶点的法线方向就是这三根法线的平均值( A vertex's vertex normal is average of three face normals)。
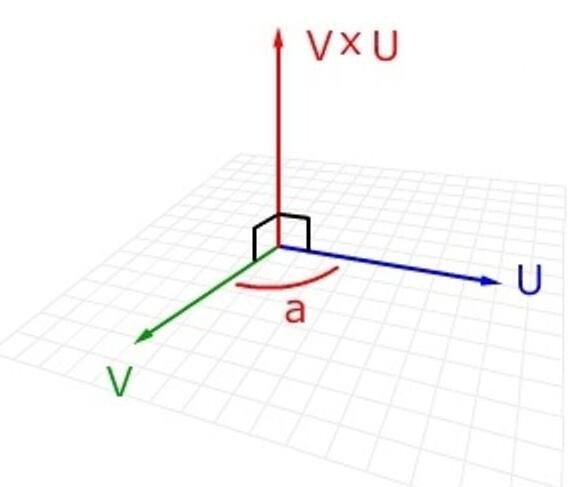
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量的和垂直。