所谓渲染中的运动模糊无非就是差值算法。目前使用的比较多的主要有两种。第一种就是上面说到的直接使用速度来线性差值,这种方法会计算每一个点的速度方向,计算出前一帧或者后一帧的位置,并与当前帧在两点之间进行线性采样这样就得到了运动的感觉。另一种直接是算的帧与帧之间的位移,然后把几何体变形差值来算出中间的模糊状态。其实两种方法大同小异,但是后者有一个好处是如果渲染目标是有substep的话,那么会优先使用这些substep找到帧之间的中间值,那么substep就是我们得到准确运动效果的模糊。
在详说之前先看三张图的对比:



三张图都是用的同一个点的旋转动画,在这里为了作比较我把相机shutter开为1,也就是每帧之间是全长度差值的,另外模糊偏移是设置为的0,也就是前帧取一半后帧取一半来完成当前帧的模糊渲染。第一张图直接使用的速度值来进行插值模糊,能够很明显的看得出最后形成的图案连一个闭环都算不上。第二张图使用的是传统的位移变换插值,但是在每一帧之间的substep都是线性变换的,所以能够看出来一个圆环高速转起来结果变成了一个类似多边形的效果。最后一个是用我的方法计算出来的中间值,虽然不是绝对完美的匹配了圆环,但是曲线的效果非常明显,而且已经非常符合眼睛看到的残影。
如果我们在houdini里面使用的是脚本或者表达式来驱动的动画,我们大可不必为中间的substep担心,因为houdini会自己帮我们找到准确的位置,因为所有路径都是计算出来的,不论精确到哪一个时间点上。而如果我们把这些动画以几何体的形式转存到硬盘上,那么上面说的substep就会全部转成每一帧之间线性的插值(像图2)。而且这一点还是在拓扑和点数前后保持一致的前提下。在后面会讲怎么解决像粒子在时间线上点数不断变化的问题。我们可以把线性的位移动画直接提取到chop里面来进行更高级的非线性插值,从而达到运动模糊能够有圆滑的曲线感。如下图:
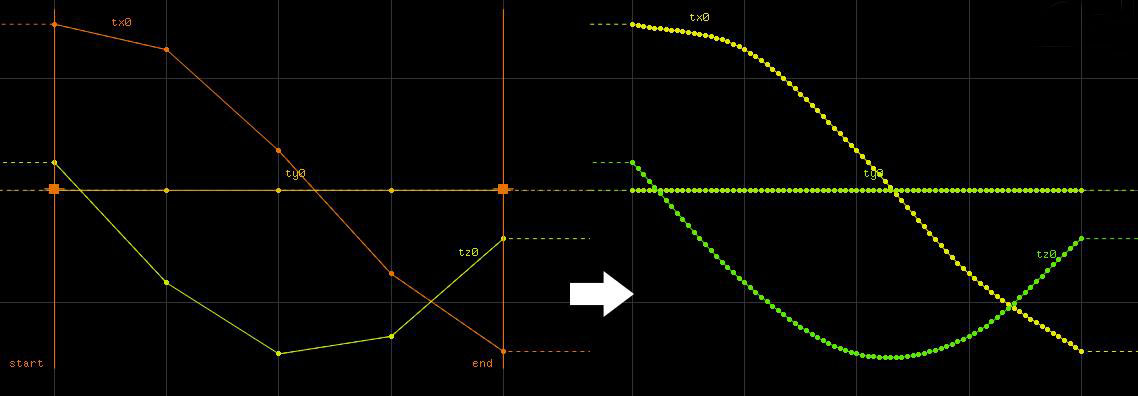
通过把P点数据以动画形式导入进去得到t[xyz]三条曲线,以当前帧为基础,分别多导入前后两帧(其实前后一桢也可以,不过两帧更安全),在使用resample节点在段与段之间加入新点。这里值得注意的是要使用cubic,也就是这个带来了非线性的感觉。而且这个方法也确保了之前的所有控制点都在曲线上,所以不会改变每个整数帧上点的位置。
插值的方法就是这个,再来讲一讲另一个用在火花上非常实际的问题,那就是点数不稳定的问题。上面所讲的方法一定是要建立在前后帧点数一定的前提下。所以如果粒子的生命不够动画长度的话,很可能就会使上面的方法直接死掉。不过这个问题也有一个突破口,那就是粒子有个点属性叫id。当动画调整完之后,我们拉到最后一帧可以很明确的知道最后一个id数是多少,这个数也代表了粒子一共出现过多少个。
解决这个问题的方法就是首先直接生成id最大数量的默认点,位置随便在哪都好(最好把初始位置放在发射源的中心点)。然后通过比对id数是否和自己的点数一致,一致的话把粒子的位置和其他必要属性直接传个生成的这个固定点,这样就从变的点交接到了固定数目的点上去了。这个过程我使用的一点点vex:
复制代码
1 int popNum = npoints(1);
2 vector startPos = point(2, "P", 0);
3
4 for(int i = 0; i < popNum; i++){
5 int popId = point(1, "id", i);
6 if(@ptnum == popId){
7 vector popPos = point(1, "P", i);
8 @P = popPos;
9 f@alpha = 1;
10 break;
11 }else{
12 @P = startPos;
13 f@alpha = 0;
14 }
15 }
复制代码
这里的alpha是想让那些还没有动的点暂时渲染时不可见。
我之前说最好把初始位置放在发射源的中心点,是因为其实这个方法结合上面的模糊差值还是有一个小小的问题,那就是从默认点位置变换到粒子发射的点上,中间这段距离也会产生模糊,但是这个模糊是绝对不正确也不需要的,但好在粒子一般都是从物体表面或者体积内部发射出来的,我们完全可以用发射源来遮住这一帧的错误。
下面看看火花的效果对比,为了看效果快门还是用的1,但是明显能看出孰优孰劣了:





